Today we will learn the Quick Sort Program in C.So before starting you should have a little bit knowledge about quick sort. So,
Table of Contents
What is Quick Sort?
Quicksort is a very efficient sorting method. It is also called “partition Exchange Sort”. The strategy used here is “Divide and Conquer” i.e, we successively partition the list into smaller lists and apply the same procedure to the sub-list.
Procedure:
We consider one element at a time (pivot) and place it in its correct position. The pivot is placed such that all elements to the left of the pivot are less than the pivot and all elements to the right are greater.
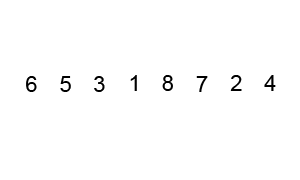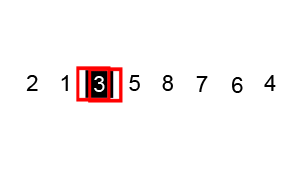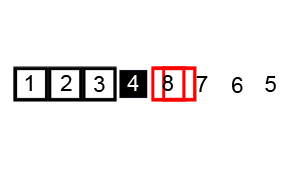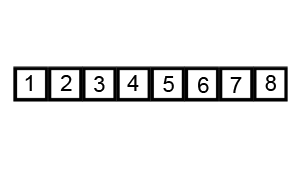
This partitions the array into two parts-left partition and right partition. The same method is applied for each of the partition. The process continues till no more partition can be made.
Note: any element can be chosen as the pivot.
We shall be considering the first element as the pivot element. The recursive function is similar to Mergesort seen earlier. However, in quick sort, we do not divide into two equal parts but partition on the basis of the pivot element.
The function sorts elements a[lb] to a[ub] where lb stands for lower bound and ub stands for the upper bound.
void Quicksort( int a[], int lb,int ub)
{
int j;
if(lb<ub)
{
j=Partition(a,lb,ub); //partition the array
Quicksort(a,lb,j-1); //sort first partition
Quicksort(a,j+1,ub); //sort second partition
}
}
Now we must write the function to partition the array. We shall choose the first element of the sub-array as the pivot and find its correct position in the sub-array.
We will be using two variables i.e down and up for moving down and up the array.
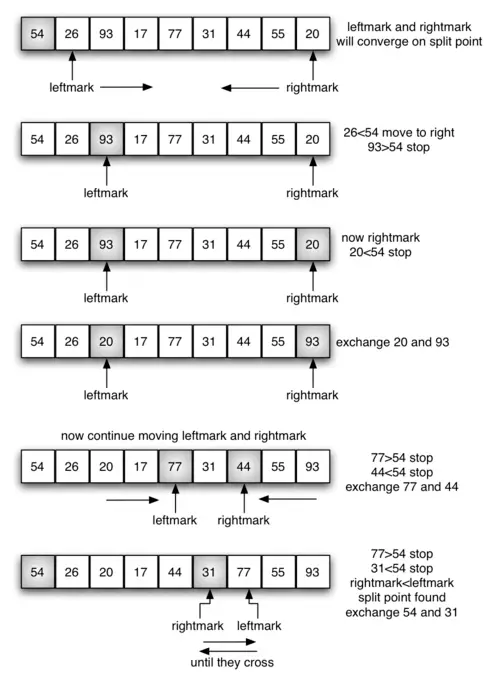
Algorithm for Partitioning:
1st Step: START.
2nd Step: down=lb.
3rd Step: up=ub.
4th Step: pivot=A[lb].
5th Step: While (A[down]<=pivot && down<ub) and down++.
6th Step: While (A[up]>pivot && up>lb) and up–.
7th Step: If(down<up) interchange A[down] and A[up]. and go to step 5.
8th Step: Interchange A[up] and A[lb].
9th Step: Return up.
10th Step: STOP.
In this Algorithm, we want to find the position of pivot i.e A[lb].
We use two pointers up and down initialized to the first and last elements respectively.
We repeatedly increase down as long as the element is < pivot i.e A[down]<pivot.
Also repeatedly decrease up as long as the element is >pivot i.e A[up]>pivot.
If up and down cross each other i.e up <=down, the correct position of the pivot is up and A[up] and pivot are interchanged.
If up and down do not cross, A[up] and A[down] are interchanged and the process is repeated till they do not cross or coincide.
For Example: Sort 55,7,80,32,18,23,82,62

First Partition: 18 7 23 32.
Second Partition: 80 82 62.
Applying the algorithm to the first partition:

Efficiency of Quicksort:
Best Case Behavior:
The best-case behaviour occurs if there are n elements such that every time a pivot is positioned, the partitions are of equal sizes.
Thus, we have to sort two sub-arrays each of size about n/2. Each of these will be partitioned into two arrays of sizes n/4. each as shown below.
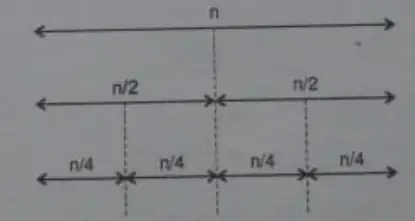
The total number of iterations taken in log2n (here 2 is the base). In each Iteration, the total number of elements to be compared is n.
Therefore, the Best case Time complexity= O(n log2n). The best-case time complexity is achieved if the median is chosen as the pivot. This will ensure that the array splits into equal parts each time.
Worst Case Behavior:
This occurs when the pivot does not partition the array. All elements are either in the left or the right partition. This will happen when the pivot either the smallest or the largest element.
Thus, there are n iterations. The total number of comparisons will be n+(n-1)+(n-2)+…+1=n(n+1)/2.
Therefore, the Worst-case Time complexity=O(n^2). This occurs when the array is already sorted or if the elements are in the reverse order. However, in all cases, it performs efficiently.
Advantages:
It is a very efficient sorting method.
No additional data structure is required.
It is in-place sorting method.
Disadvantages:
It is not a stable sorting method.
Applications:
Defence.
Medical Monitoring.
Control for Aircraft etc.
1. Quick Sort Program in C
In this program, the compiler will ask the user to enter the number of elements and then after sorting the compiler will print all the sorted elements on the screen.
Note: Consider up(upper bound) as high and lb(lower bound) as low.
#include<stdio.h>
int n;
int main()
{
int arr[30],l,r,i;
void quick_sort(int arr[],int,int);
printf("\nInput number of elements: ");
scanf(" %d",&n);
printf("\nInput array values one by one: ");
for(i=0;i<n;i++)
scanf(" %d",&arr[i]);
l=0; r=n-1;
quick_sort(arr,l,r);
printf("\nThe quick sorted array is: ");
for(i=0;i<n;i++)
printf(" %d",arr[i]);
printf("\n");
}
void quick_sort(int arr[],int low,int high)
{
int temp,left,right,x,k;
if(low>=high)
return;
else
{
x=arr[low];
right=low+1;
left = high;
while(right<=left)
{
while(arr[right]<x && right <= high)
{
right ++;
}
while(arr[left]>x && left > low)
{
left--;
}
if(right<left)
{
temp=arr[right];
arr[right]=arr[left];
arr[left]=temp;
right++;
left--;
}
}
arr[low]=arr[left];
arr[left]=x;
quick_sort(arr,low,left-1);
quick_sort(arr,left+1,high);
}
}
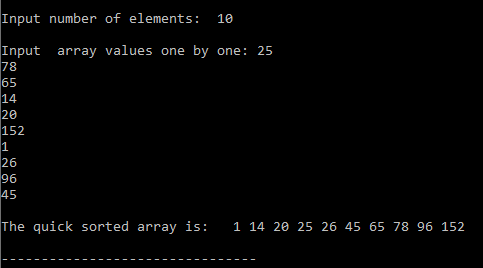
Output:
2. Quick Sort program in C Using Recursion
The program is said to be recursive if the function calls itself symmetrically.
#include <stdio.h>
void quicksort (int [], int, int);
int main()
{
int list[50];
int size, i;
printf("Enter the number of elements: ");
scanf("%d", &size);
printf("Enter the elements to be sorted:\n");
for (i = 0; i < size; i++)
{
scanf("%d", &list[i]);
}
quicksort(list, 0, size - 1);
printf("After applying quick sort\n");
for (i = 0; i < size; i++)
{
printf("%d ", list[i]);
}
printf("\n");
return 0;
}
void quicksort(int list[], int low, int high)
{
int pivot, i, j, temp;
if (low < high)
{
pivot = low;
i = low;
j = high;
while (i < j)
{
while (list[i] <= list[pivot] && i <= high)
{
i++;
}
while (list[j] > list[pivot] && j >= low)
{
j--;
}
if (i < j)
{
temp = list[i];
list[i] = list[j];
list[j] = temp;
}
}
temp = list[j];
list[j] = list[pivot];
list[pivot] = temp;
quicksort(list, low, j - 1);
quicksort(list, j + 1, high);
}
}
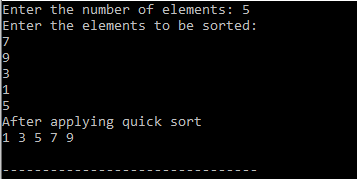
Output:
Also Read:
- C Program to Make Simple Calculator
- Armstrong Number Program in C
- Fibonacci Series Program in C
- Decimal to Binary Conversion Program in C
- Reverse a String in C
- Program to Reverse a Number in C
- Hello World Program in C
- Palindrome Program in C
- Leap Year Program in C
- Factorial Program in C
- Prime Number Program in C
- Program to print prime numbers from 1 to n
- Anagram program in C.
- Calculate LCM Program in C.
- Addition of Two Numbers in C
- Matrix Multiplication Program in C.
- Playfair Cipher Program in C.
- GCD Program in C.
- Tower of Hanoi in C.
- First Fit Program in C
- Swapping of two numbers in C
- Menu Driven Program in C.
- Odd or Even number program in C
- Round Robin Program in C
- Simple Interest Program in C
- Quadratic Equation Program in C.
- Bubble Sort Program in C.
- Insertion Sort Program in C.
- Merge Sort Program in C.
- Linear Search Program in C.
![FIFO Page Replacement Algorithm in C [ Program With Explanation]](https://learnprogramo.com/wp-content/uploads/2021/12/FIFO-PAGE-REPLACEMENT-ALGORITHM-IN-C-1-500x383.png)

