Binary Search Program in C | Binary Search in C

Today we will learn Binary Search Program in C. So before getting started, we will make you know about binary search. What exactly binary search is?

What is Binary Search?

This is a very efficient searching method used for linear or sequential data (files, arrays or linked lists).

Pre-requirement: data has to be in the sorted order.

Procedure:

In this method, the set of elements is partitioned into two equal parts and the required key is compared with the key of the middle record. If a match is found, the search terminates.

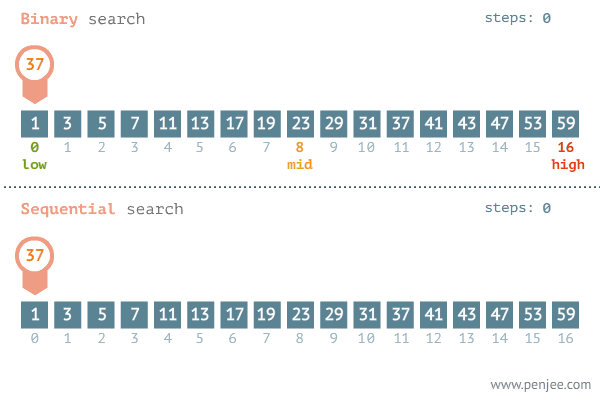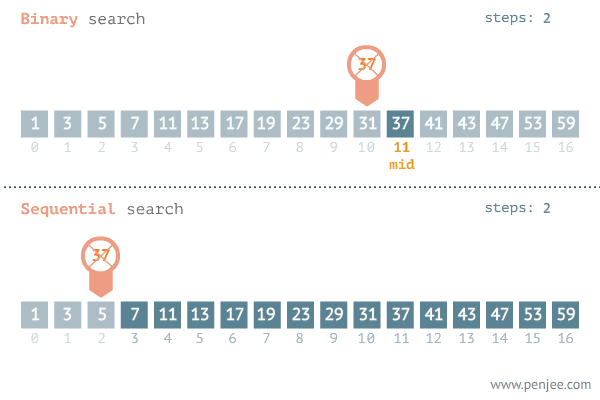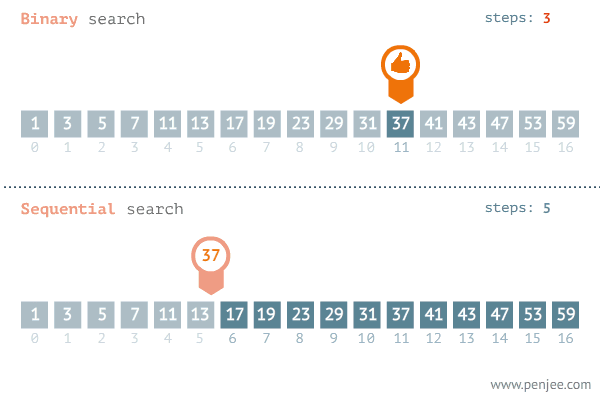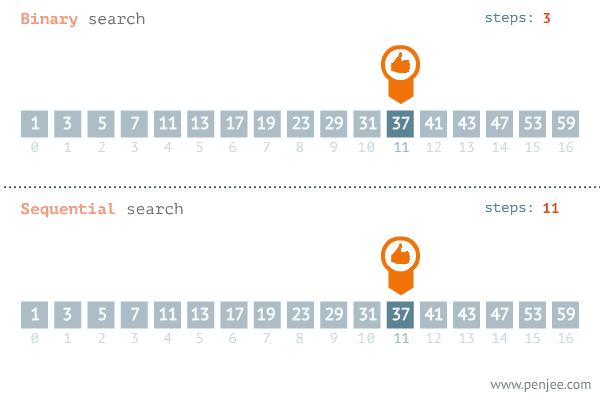
If the key is less than the middle key, the search proceeds in the top half of the table.

And If the key is greater than the middle key, the search proceeds in the same way in the lower half of the table.

The process continues until no more partitions are possible.

Thus every time a match is found, the remaining table size to be searched reduces the half.

Binary Search Algorithm:

1st Step: START.

2nd Step: Accept key to be searched.

3rd Step: top=0.

4th Step: bottom=n-1.

5th Step: mid= (top+bottom) / 2.

6th Step: If k(mid)==key then Display “Record found at position mid” then go to step 10.

7th Step: If key<k(mid) then bottom=mid-1 else, top=mid+1.

8th Step: If top<=bottom then go to step 5.

9th Step: Display “Record not found”.

10th Step: STOP.

Efficiency:

After 0 Comparisons -> Remaining file size = n.

After 1 Comparisons -> Remaining file size = n/2 = n/2^1.

And after 2 Comparisons -> Remaining file size = n/4 = n/2^2.

And after k Comparisons -> Remaining file size = n / 2^k.

The process terminates when no more partitions are possible i.e remaining file size = 1 -> n/2^k =1. i.e, k=log2n (2 is at base).

Thus, the time complexity is O(log2n) which is very efficient.

Example: If there are 1024 records in the file and the record with the required key is not present (worst case), the maximum number of comparisons will be log2(1024) = 10.

Advantages:

Time complexity is O(log2n) which is very efficient.

Does not require any additional data structure.

Disadvantages:

Data has to be in sorted manner.

This method can only be applied to the sequential or linear data structure.

The following program illustrates a binary search on a set of n elements. The elements are sorted using the bubble sort method studied earlier.

1. Binary Search Program in C

In this program, the compiler will ask the user to enter the elements. After the user enters the number to find then the compiler will start to find the number in the array. If the number is found then the compiler will print the number found at position i else print number not found.

Consider top=high and bottom=low.

#include <stdio.h>
int main()
{
int i, low, high, mid, n, key, array[100];
printf("Enter number of elements\n");
scanf("\n%d",&n);
printf("Enter %d integers\n", n);
for(i = 0; i < n; i++)
scanf("%d",&array[i]);
printf("Enter value to find\n");
scanf("%d", &key);
low = 0;
high = n - 1;
mid = (low+high)/2;
while (low <= high) {
if(array[mid] < key)
low = mid + 1;
else if (array[mid] == key) {
printf("%d found at location %d.\n", key, mid+1);
break;
}
else
high = mid - 1;
mid = (low + high)/2;
}
if(low > high)
printf("Not found! %d isn't present in the list.\n", key);
return 0;
}

Output:

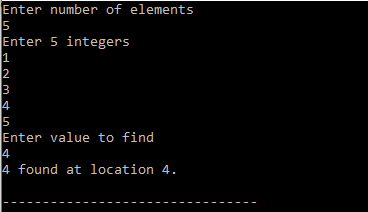
Note: This algorithm will not work if the numbers are not sorted.

Explanation:

We first, consider in the number of components the user selection wants and keep it into n. Next, we take the components from the user. Then, we choose the amount to be hunted by the array and keep it at the key.

We assign 0 to the very low factor that’s the first indicator of an array and n-1 into the large element, that’s the previous element from the array. There’s a while loop that checks if none is significantly less then high to ensure the range still has components inside.

If low is higher afterwards, high then the selection is empty. Within the while loop, we first assess whether the component at the middle is significantly less than the primary value(array[mid] < key).

If so, we then assign reduced the worth of mid +1 since the essential value is higher then mid and can be more towards the higher side.

And if that is untrue, we then check if mid is equivalent to the key. If so, we publish and break from this loop. If these conditions do not match then we delegate high the worth of mid-1, meaning that the secret is smaller compared to mid.

The previous part checks if none is higher then high so that there are no more elements left in the array.

2. Binary Search Using Recursive Function

#include <stdio.h>
int binaryScr(int a[], int low, int high, int m)
{
if (high >= low) {
int mid = low + (high - low) / 2;
if (a[mid] == m)
return mid;
if(a[mid] > m)
return binaryScr(a, low, mid - 1, m);
return binaryScr(a, mid + 1, high, m);
}
return -1;
}
int main(void)
{
int a[] = { 5,10,15,20,25,30,35 };
int i,m;
for(i=0;i<5;i++)
{
printf(" \n%d",a[i]);
}
printf(" \n");
int n = sizeof(a) / sizeof(a[0]);
printf("Enter the number to be searched\n");
scanf("\n%d", &m);
int result = binaryScr(a, 0, n - 1, m);
(result == -1);
printf("The element is not present in array");
printf("\nThe element is present at index %d",result);
return 0;
}

Output:

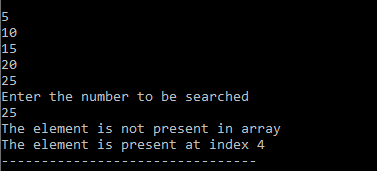
In the above program, we utilize a purpose BinaryScr to look for the component from the array. The purpose is recursively called to look for the component. We take the input from the user and keep it.

We’ve declared and initialized the selection. We ship the variety, the reduced indicator, greater indicator and the amount to be hunted to the BinaryScr purpose and assign it to result.

In the primary purpose, the ternary operator is utilized. If response =-1 then not discovered else discovered is displayed.

Also Read:

• Bubble Sort Program in C.
• Insertion Sort Program in C.
• Merge Sort Program in C.
• Quick Sort Program in C.
• Linear Search Program in C.
• Shortest Job First Program in C