Today we will learn C program for Quadratic Equation and also learn how to find the roots of a quadratic equation. So before starting you should have knowledge about the quadratic equation. So,
Table of Contents
What is Quadratic Equation?
A Quadratic Equation is any time of the equation that can be rearranged in the standard form as ax^2+bx+c=0. Where, x is the unknown variable and the a,b,c are the known numbers where a!=0.
If a=0 then the equation is said to be linear and not a quadratic equation as there is no ax^2.
The numbers a,b and c are the coefficients of the equation and can be called as quadratic coefficients.
Understanding Quadratic Equation:
The Expression under the square root sign is called as discriminant of the quadratic equation and can be represented as:
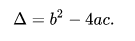
The Quadratic equation can have either one or two distinct real roots. In this case, the Discriminant determines the nature of the roots whether it is positive, negative or zero. There are three Cases to determine,
1st Case: If the Discriminant is +ve then there are exactly two distinct roots both are real numbers.
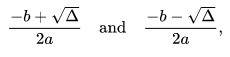
2nd Case: If the Discriminant is -ve then there are no real roots but there exists two distinct non-real roots which are complex.
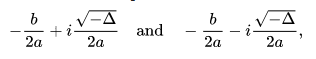
3rd Case:
If the Discriminant is 0, then there exists one real root also called as double root i.e
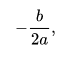
Quadratic Equation Algorithm
1 Step: Input the coefficients of the quadratic equation from the user and store in the variables a,b and c.
2 Step: Now find the Discriminant of the equation by using formula Discriminant=(b*b)-(4*a*c).
3 Step: Now compute their roots based on the nature of Discriminants.
4 Step: If discriminant>0 then, 1st root=(-b + sqrt(Discriminant)) / 2*a and 2nd root=(-b – sqrt(Discriminant)) / 2*a
5 Step: If the Discriminant==0 then 1st root=2nd root= -b/2*a. and if Discriminant is -ve then there are two distinct non-real complex roots where 1st root=-b/2*a and 2nd root=b/2*a.
Imaginary roots are given by imagine=sqrt(-Discriminant)/2*a
C Program for Quadratic Equation Using if else
In this program the compiler asks the user to enter the value of coefficients a,b and c then the program finds the roots of the quadratic equation.
#include <stdio.h>
#include<math.h>
int main()
{
float a, b, c;
float root1, root2, imaginary, discriminant;
printf("\n Please Enter values of a, b, c of Quadratic Equation :\n ");
scanf("\n%f\n%f\n%f", &a, &b, &c);
discriminant = (b * b) - (4 * a *c);
if(discriminant > 0)
{
root1 = (-b + sqrt(discriminant) / (2 * a));
root2 = (-b - sqrt(discriminant) / (2 * a));
printf("\n Two Distinct Real Roots Exists: \nroot1 = %.2f and\n root2 = %.2f", root1, root2);
}
else if(discriminant == 0)
{
root1 = root2 = -b / (2 * a);
printf("\n Two Equal and Real Roots Exists:\n root1 = %.2f and \nroot2 = %.2f", root1, root2);
}
else if(discriminant < 0)
{
root1 = root2 = -b / (2 * a);
imaginary = sqrt(-discriminant) / (2 * a);
printf("\n Two Distinct Complex Roots Exists:\n root1 = %.2f+%.2f and \nroot2 = %.2f-%.2f", root1, imaginary, root2, imaginary);
}
return 0;
}
Output:
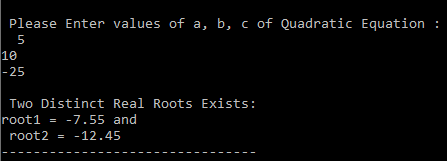
Explanation:
The user has entered the values of a=5,b=10 and c=-25.
So, the Discriminant=(b*b)-(4*a*c) / 2*a i.e (10*10)-(4*5*-25) / 2*5 so Discriminant=(100)-(-500)/10 = 5000.
1st root=-b+sqrt(Discriminant)/2*a i.e -10+sqrt(5000)/10 so the value of 1st root=-7.5
2st root=-b-sqrt(Discriminant)/2*a i.e -10-sqrt(5000)/10 so the value of 1st root=-12.45.
2. Quadratic Equation using Switch Case
#include <stdio.h>
#include<math.h>
int main()
{
float a, b, c;
float root1, root2, imaginary, discriminant;
printf("\n Please Enter values of a, b, c of Quadratic Equation : \n ");
scanf("%f%f%f", &a, &b, &c);
discriminant = (b * b) - (4 * a *c);
switch(discriminant > 0)
{
case 1:
root1 = (-b + sqrt(discriminant) / (2 * a));
root2 = (-b - sqrt(discriminant) / (2 * a));
printf("\n Two Distinct Real Roots Exists:\n root1 = %.2f and \nroot2 = %.2f", root1, root2);
break;
case 0:
switch(discriminant < 0)
{
case 1: //True
root1 = root2 = -b / (2 * a);
imaginary = sqrt(-discriminant) / (2 * a);
printf("\n Two Distinct Complex Roots Exists: \nroot1 = %.2f+%.2f and\n root2 = %.2f-%.2f", root1, imaginary, root2, imaginary);
break;
case 0: // False (Discriminant = 0)
root1 = root2 = -b / (2 * a);
printf("\n Two Equal and Real Roots Exists:\n root1 = %.2f and \nroot2 = %.2f", root1, root2);
break;
}
}
return 0;
}
Output:
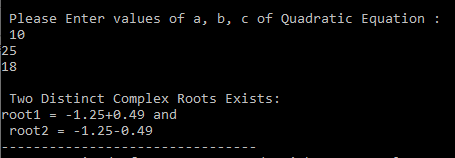
3. Finding roots using Equation
In this program the compiler will ask user to type the equation in the form of ax^2+bx+c and then the compiler will print the roots of the quadratic equation.
#include<stdio.h>
#include<math.h>
int main(){
float a,b,c;
float d,root1,root2;
printf("Enter quadratic equation in the format ax^2+bx+c: \n");
scanf("%fx^2%fx%f",&a,&b,&c);
d = b * b - 4 * a * c;
if(d < 0){
printf("Roots are complex number.\n");
return 0;
}
root1 = ( -b + sqrt(d)) / (2* a);
root2 = ( -b - sqrt(d)) / (2* a);
printf("Roots of quadratic equation are:\n %.3f ,\n %.3f",root1,root2);
return 0;
}
Output:
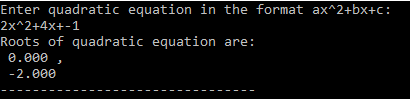
Also Read:
- C Program to Make Simple Calculator
- Armstrong Number Program in C
- Fibonacci Series Program in C
- Decimal to Binary Conversion Program in C
- Reverse a String in C
- Program to Reverse a Number in C
- Hello World Program in C
- Palindrome Program in C
- Leap Year Program in C
- Factorial Program in C
- Prime Number Program in C
- Program to print prime numbers from 1 to n
- Anagram program in C.
- Calculate LCM Program in C.
- Addition of Two Numbers in C
- Matrix Multiplication Program in C.
- Playfair Cipher Program in C.
- GCD Program in C.
- Tower of Hanoi in C.
- First Fit Program in C
- Swapping of two numbers in C
- Menu Driven Program in C.
- Odd or Even number program in C
- Round Robin Program in C
- Simple Interest Program in C
- Bubble Sort Program in C


