Today we will learn the Tower of Hanoi in C and also learn the tower of Hanoi program in C using recursion. So before starting, we will explain in detail about the Tower of Hanoi.
Table of Contents
What is Tower of Hanoi?
The Tower of Hanoi is the mathematical Puzzle. This puzzle was invented by the French mathematician Edouard Lucas in 1883.
There is a big dome situated in Banaras, that marks the middle of the world, contains a brass plate in which three diamond needles are fixed.
Each needle is cubit high and as thick as the body of a Bee.
When these needles were created God placed sixty-four discs of pure gold on one of this needle. The greatest disc resting on the brass plate, along with the others getting smaller and smaller up into the upper.
This Tower is also called the Tower of Bramah Puzzle.
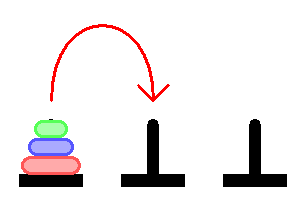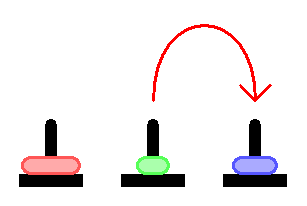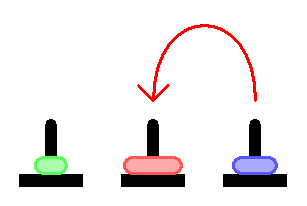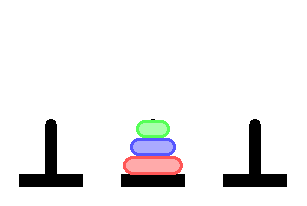
Day and night unceasingly the priests move the disks from 1 diamond needle to another in accordance with the fixed and immutable laws of Bramah.
The priest on duty must not transfer more than 1 disk at a time and he should put this disk onto a needle so that there’s not any more smaller disk under it.
According to the legend when the last move of the puzzle will compete the world will vanish.
The main Objective of the puzzle is to move the entire stack on the next rod.
Initial State:
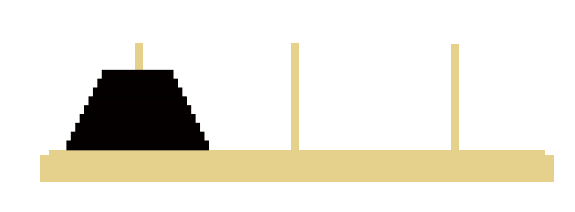
Goal State:
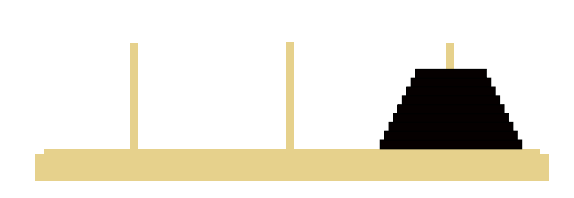
Rules of Hanoi Puzzle:
Only one disk may move at a time.
Each move consists of taking upper disk of one of the peg and put that disk on the other peg on top of the other disks.
None of the disk should place on top of smaller disk.
Applications of Tower of Hanoi:
There exists a version of the Job Known as Tower of London for neuropsychological analysis and therapy of executive purposes.
The Tower of Hanoi can be used as a Backup spinning strategy when performing computer information Backups where multiple Tapes and media are included.
As stated previously, the Tower of Hanoi is a favourite for instructing recursive algorithms to begin programming students. A pictorial version of the puzzle is programmed to the emacs editor, obtained by scanning M-x Hanoi.
The Tower of Hanoi can be utilized as a memory evaluation by neuropsychologists hoping to appraise amnesia.
One Disk Solution:
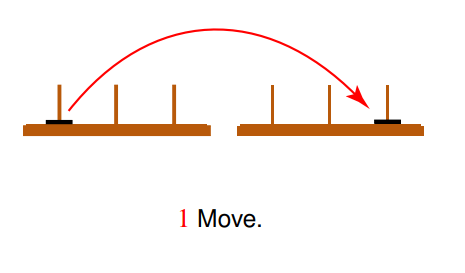
It contains only one move.
Two Disk Solution:
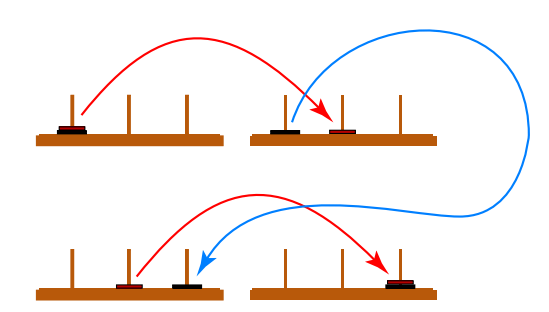
Note that we perform a solution to one disk tower two times one at the top row and second in the bottom row. Between rows, we move the bottom disk. Therefore we require 2*1+1=3 Moves.
Three Disk Solution:
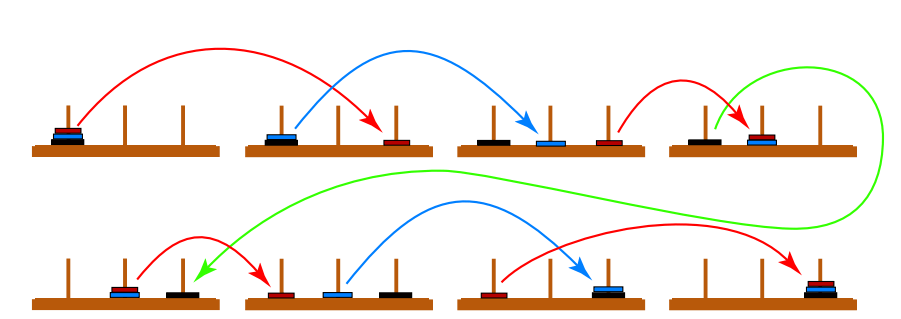
Note that we perform the solution for two disk tower two times once in the top row and once in the bottom row. Between rows, we moved to disk. Therefore we require 2(2*1+1)+1=7 Moves.
Nth Disk Analysis:
Let M(n) denotes no if legal moves required to complete the tower of Hanoi puzzle which consist of n disks. Before the largest i.e nth disk can be moved to rightmost peg and (n-1) i.e remaining peg must move to the centre peg.
So this requires M(n-1) legal moves because these disks must be somewhere.
Thus we obtain relation of recursion i.e M(n)=2M(n-1)+1.
Tower of Hanoi Solution:
Referring to the solution for a single disk M(1)=1.
The recursion relation M(n)=2M(n-1)+1.
which defines the solution M(n)=2^n-1.In the algorithms, this will be called exponential or O(2^n).
But the difficulty us that they grow quickly out of hand.1 century is equivalent to 4.5+10^9 seconds. So the age of the universe is 4 x 10^17 seconds.
If the number of disks is odd then the first move should be transferred to the top of the right peg.
And if the number of disks is even then the first move should be transferred to the top of the centre peg.
So the puzzle is solved, The length of the shortest solution path to nth disk puzzle is 2^n.
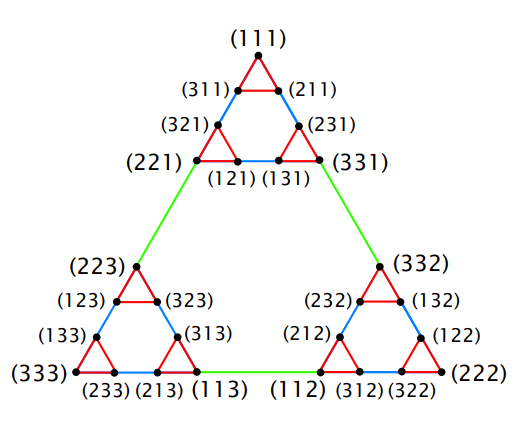
State Representation Using five disk Puzzle:
Notation (2 1 3 1 1) indicates that
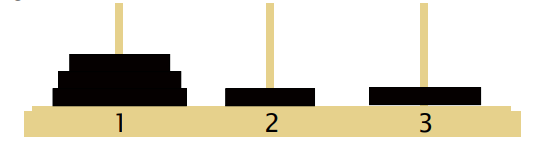
The smallest disk is on peg 2 (centre peg). The next larger disk is on peg 1 (left peg) and the next larger disk is on peg 3 (right peg). The next larger disk is on peg 1 and the next largest disk is on peg 1 which is largest.
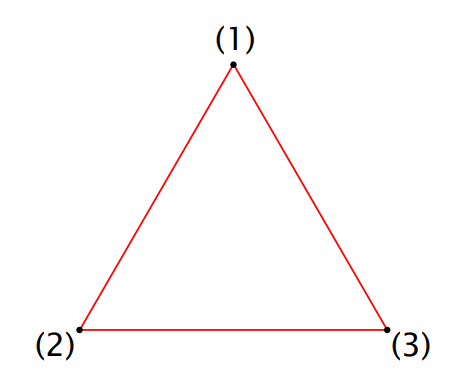
State Graph:
Each State is represented by a labeled vertex and legal moves are represented by edges.
1 Disk:
2 Disk:
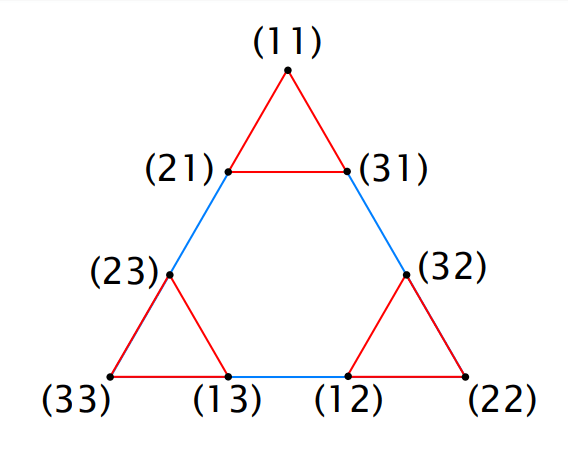
3 Disk:
1. Tower of Hanoi Program in C
#include<stdio.h>
int main ()
{
int n;
printf("Enter number of disks required: \n");
scanf ("%d", &n);
TOH (n, 'A', 'B',' C');
return 0;
}
void TOH (int n, char src, char spare, char dest)
{
if (n==1)
printf("Move from %c to %c \n", src, dest);
else
{
TOH(n-1, src, dest, spare) ;
TOH(1, src, spare, dest);
TOH(n-1, spare, src, dest);
}
}Output:
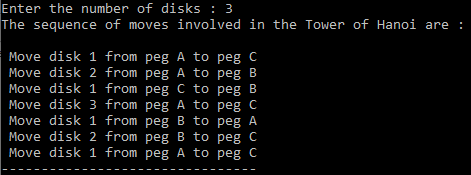
In the above example we have used 3 disks.
2. Tower of Hanoi in C Using Recursion
When the function calls itself is called recursion. In this program, we have declared the user-defined function called towers().
#include <stdio.h>
void towers(int, char, char, char);
int main()
{
int num;
printf("Enter the number of disks : ");
scanf("%d", &num);
printf("The sequence of moves involved in the Tower of Hanoi are :\n");
towers(num, 'A', 'C', 'B');
return 0;
}
void towers(int num, char frompeg, char topeg, char auxpeg)
{
if (num == 1)
{
printf("\n Move disk 1 from peg %c to peg %c", frompeg, topeg);
return;
}
towers(num - 1, frompeg, auxpeg, topeg);
printf("\n Move disk %d from peg %c to peg %c", num, frompeg, topeg);
towers(num - 1, auxpeg, topeg, frompeg);
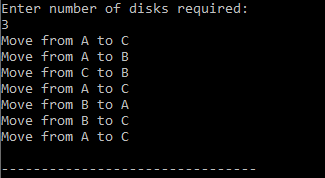
}Output:
Also Read:
- C Program to Make Simple Calculator
- Armstrong Number Program in C
- Fibonacci Series Program in C
- Decimal to Binary Conversion Program in C
- Reverse a String in C
- Program to Reverse a Number in C
- Hello World Program in C
- Palindrome Program in C
- Leap Year Program in C
- Factorial Program in C
- Prime Number Program in C
- Program to print prime numbers from 1 to n
- Anagram program in C.
- Calculate LCM Program in C.
- Addition of Two Numbers in C
- Matrix Multiplication Program in C.
- Playfair Cipher Program in C.
- GCD Program in C.
- First Fit Progam in C.


