Prime Number Program in C | Program for Prime Number in C

Today we will learn the prime number program in c and how to check whether the given number is prime or not. So before learning, you should have a piece of knowledge about a prime number.so first of all,

Table of Contents

What are Prime Numbers?

Any natural number which can be divisible by itself or the number which has only two factors i.e 1 and the number itself are called prime numbers.

For example 2,3,5,7,11 and so on…

Note: The number 2 is only even prime number because most of the numbers are divisible by 2.

Program to check a single number is prime or not in c:

In this program, we will take input from the user and check whether the given input number is prime or not.

#include<stdio.h>  
int main(){    
int n,i,m=0,flag=0;    
printf("Enter the number to check prime:");    
scanf("%d",&n);    
m=n/2;    
for(i=2;i<=m;i++)    
{    
if(n%i==0)    
{    
printf("Number is not prime");    
flag=1;    
break;    
}    
}    
if(flag==0)    
printf("Number is prime");     
return 0;  
 }

Output:

C Program to check given number is prime or not using for loop:

In this program, we will ask the user to input n number and check whether the given n number is prime or not using for loop.

#include <stdio.h> 

main() 
{
  int n, i, c = 0;
  printf("Enter any number n to check:");
  scanf("%d", &n);

  for (i = 1; i <= n; i++) 
  {
      if (n % i == 0) 
	  {
         c++;
      }
  }

  if (c == 2) 
  {
  printf("given n is a Prime number");
  }
  else 
  {
  printf("given n is not a Prime number");
  }
  return 0;    
}

Output:

Explanation:

let us consider n=5 for loop becomes for(i=1; i<5; i++)

1st Iteration: for(i=1; i<=5; i++) in 1st iteration i is incremented i.e the value of i for the next iteration is 2.If (n%i==0) then c is incremented i.e (5%1==0) then c is incremented.Here, (5%1=0) so c is incremented i.e c=1.

2nd Iteration: for(i=2;i<=5;i++) in 2nd iteration i is incremented i.e the value of i for the next iteration is 3.If (n%i==0) then c is incremented i.e (5%2==0) then c is incremented.here,(5%2!=0) so c is not incremented i.e c=1.

3rd Iteration: for(i=3;i<=5;i++) in 3nd iteration i is incremented i.e the value of i for the next iteration is 4.If (n%i==0) then c is incremented i.e (5%3==0) then c is incremented.Here,(5%3!=0) so c is not incremented i.e c=1.

4th Iteration: for(i=4;i<=5;i++) in 4th iteration i is incremented i.e the value of i for the next iteration is 5.If (n%i==0) then c is incremented i.e (5%4==0) then c is incremented.Here,(5%4!=0) so c is not incremented i.e c=1.

5th Iteration: for(i=5;i<=5;i++) in 5th iteration i is incremented i.e the value of i for the next iteration is 6.If (n%i==0) then c is incremented i.e (5%5==1) then c is incremented.Here,(5%5=0) so c is incremented i.e c=2.

6th Iteration: for(i=6;i<=5;i++) in 6th iteration the value of i is 6 which is greater than n i.e i>n(6>5) so the for loop is terminated.Here c=2 so the given number is prime number.

C Program to check given number is prime or not using while loop:

In this program we will ask user to enter the number which user want to check whether it is prime or not and then check it using while loop.

#include <stdio.h> 
int main()
{
int i = 2, Number, count = 0; 
printf("\n Please Enter number to Check Prime or not \n");
scanf("%d", &Number);
while(i <= Number/2)
   {
     if(Number%i == 0)
     {
   count++;
	break;
      }
      i++;	
   }
   if(count == 0 && Number != 1 )
   {
   	printf("\n %d is a Prime Number", Number);
   }
   else
   {
 	printf("\n %d is Not a Prime Number", Number);
   }
  return 0;
}

Output:

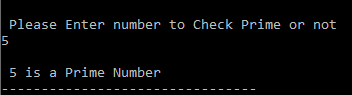
check whether the given number is prime or not

In above program we just replace the for loop instead we add while loop.

C program to check the given number is prime or not using functions:

In this program, we will use the function find_factors to check whether the given number is prime or not.

#include <stdio.h>
int find_factors(int Number)
{ 
  int i, Count = 0; 
  for (i = 2; i <= Number/2; i++)
   {
    if(Number%i == 0)
     {
       Count++;
     } 
   }
   return Count;
}
int main()
{
  int i, Number, count = 0;  
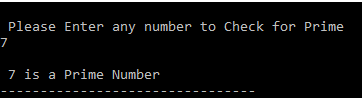
  printf("\n Please Enter any number to Check Prime or not \n");
  scanf("%d", &Number);
  count = find_factors(Number);
   if(count == 0 && Number != 1 )
   {
   	printf("\n %d is a Prime Number", Number);
   }
   else
   {
   	printf("\n %d is Not a Prime Number", Number);
   }
  return 0;
}

Output:

Sieve Of Eratosthenes Algorithm:

In this algorithm, we first declare the numbers from [2:n]. We mark all the multiples of 2 as the number 2 is composite. A proper multiple of number x, which is multiple of number x and divisible by x.

Then we mark the number which hasn’t be composite.for example 3 which is not composite,It means that 3 is a prime number.

Now we will see the program for Sieve Of Eratosthenes Algorithm.

int count_primes(int n) {
    const int S = 10000;
    vector<int> primes;
    int nsqrt = sqrt(n);
    vector<char> is_prime(nsqrt + 1, true);
    for (int i = 2; i <= nsqrt; i++) {
        if (is_prime[i]) {
            primes.push_back(i);
            for (int j = i * i; j <= nsqrt; j += i)
                is_prime[j] = false;
        }
    }
    int result = 0;
    vector<char> block(S);
    for (int k = 0; k * S <= n; k++) {
        fill(block.begin(), block.end(), true);
        int start = k * S;
        for (int p : primes) {
            int start_idx = (start + p - 1) / p;
            int j = max(start_idx, p) * p - start;
            for (; j < S; j += p)
                block[j] = false;
        }
        if (k == 0)
            block[0] = block[1] = false;
        for (int i = 0; i < S && start + i <= n; i++) {
            if (block[i])
                result++;
        }
    }
    return result;
}

Here we have a program that counts the no of primes smaller than or equal to n.

Also Read: