Table of Contents
What is Operator Precedence in C language?
The Operator Precedence in C determines whether which operator should perform first in the expression which contains multiple operators.
For evaluation of expressions having more than one operator, there are certain precedence and associativity rules are defined in C language.
The operators within c language are grouped hierarchically. According to the predefined rule of priority for the operators, this rule of priority of operators is called Operator Precedence.
Operations with higher precedence are carried out before operations having lower precedence. The natural order of evaluation can be altered, however, through the use of parentheses.
Another important term in operators is associativity.
Associativity is the order in which consecutive operations within the same precedence group are carried out. Associativity is used when two operators of the same precedence appear in an expression.
The Associativity can be either Left to Right or Right to Left.
Precedence and Associativity are two characteristics Of operators that determine the evaluation order of subexpressions in the absence of brackets.
Let us see what these rules are and why are they required:
Consider example, 10 + 20 * 30 is calculated as 10+(20 * 30) and not as (10 + 20) * 30. Since * has the highest precedence than +.
Consider another example, ‘*’ and ‘/’ have the same precedence and their associativity is Left to Right, so the expression “100 / 10 * 10” is treated as “(100 / 10) * 10”.
Operator Precedence Chart is given below:
Precedence Chart
| Operator | Description | Associativity |
|---|---|---|
| ( ) | Parentheses | Left-to-Right |
| [ ] | Brackets | Left-to-Right |
| . | Member Selection via Object Name. | Left-to-Right |
| -> | Member Selection via Pointer. | Left-to-Right |
| ++,– | Postfix increment/decrement | Left-to-Right |
| ++ — | Prefix increment/decrement | Right-to-Left |
| + – | Unary plus/minus | Right-to-Left |
| !~ | Logical negation/bitwise complement | Right-to-Left |
| (type) | Type Casting | Right-to-Left |
| * | Dereference | Right-to-Left |
| & | Address | Right-to-Left |
| sizeof | Determine size in bytes | Right-to-Left |
| * / % | Multiplication/Division/Modulus | Left-to-Right |
| + – | Addition/Subtraction | Left-to-Right |
| << >> | Bitwise Left Shift and Right Shift | Left-to-Right |
| < <= | Relational Less than or equal to | Left-to-Right |
| > >= | Relational Greater than or equal to | Left-to-Right |
| == != | Relation is equal to or not equal to | Left-to-Right |
| & | Bitwise AND | Left-to-Right |
| ^ | Bitwise ex-OR | Left-to-Right |
| | | Bitwise OR | Left-to-Right |
| && | Logical AND | Left-to-Right |
| || | Logical OR | Left-to-Right |
| ? : | Ternary Conditional | Right-to-Left |
| = | Assignment | Right-to-Left |
| += -= | Addition/Subtraction Assignment | Right-to-Left |
| *= /= | Multiplication/Division Assignment | Right-to-Left |
| %= &= | Mudulus/Bitwise AND Assignment | Right-to-Left |
| ^= |= | Bitwise exclusive or inclusive OR Assignment | Right-to-Left |
| <<= >>= | Bitwise Left or Right Assignment | Right-to-Left |
| , | Comma | Left-to-Right |
Precedence and associativity of postfix ++ and prefix ++ are different. Comma has the least precedence among all operators and should be used carefully.
The steps to convert a given valid C expression to its mathematical form and to evaluate it are as follows:
Step 1: First determine the order in which the operators are bound to their operands by applying the precedence and associativity rules.
Note that after an operator is bound to its operand(s), that sub-expression is considered as a single operand for the adjacent operators.
Step 2: Obtain the equivalent mathematical equation for given C expression by following the operator binding sequence,(obtained in step 1).
Step 3: Determine the value of the given expression by evaluating operators in the binding sequence.
The above steps to determine operator binding in an arithmetic expression are explained below with the help of the expression -a+b*c-d/e+f.
Step 1:
The unary operators (unary +, unary -, ++ and –) have the highest precedence and right-to-left associativity. Thus, the given expression is first scanned from right to left and unary operators, if any, are bound to their operands.
The order is indicated below the expression as follows:
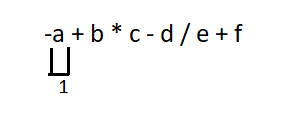
Step 2:
The multiplicative operators(*, / and %) have the next highest precedence and left-to-right associativity. Thus, the expression is scanned from left-to-right and the multiplicative operators, if any, are bound to their operands as shown below:
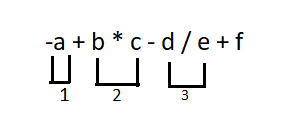
Step 3:
The additive operators (+ and -) have the next highest precedence and left-to-right associativity. Hence, the expression is scanned from left-to-right and the addictive operators, if any, are bound to their operands as shown below:
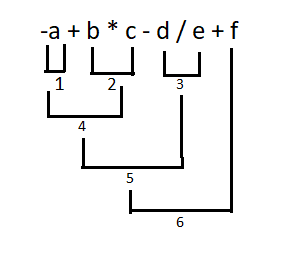
Step 4:
Now we can write the mathematical equation for the given C expression by following the operator binding sequence as shown below:
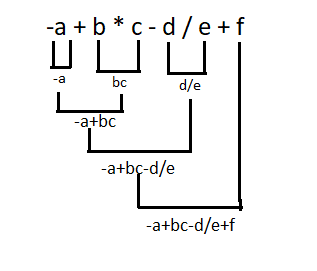
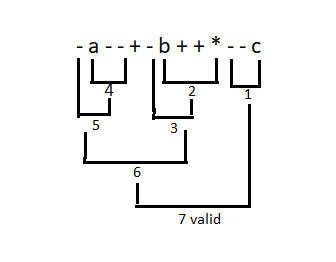
Consider a more complex arithmetic expression: -a–+-b++*–c.
This expression appears to be invalid due to the excessive use of operators. It contains three operands a, b and c and seven operators, five of which are unary (-, ++ and –) and the other two are binary operators (+ and *). However, using the operator binding steps, we can easily verify that it is a valid expression:
Also Read:


